Die notwendige Bedingung für ein Maximum einer Funktion $U\left( {x,y} \right)$ zweier Variablen

$${\rm{d}}U = {{\partial U} \over {\partial x}}{\rm{d}}x + {{\partial U} \over {\partial y}}{\rm{d}}y = 0 \tag{1}$$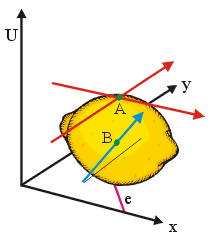

erkennt man graphisch in Punkt A in Abbildung 1 darin wieder, dass marginale Bewegungen parallel zu den Achsen den Funktionswert konstant lassen (das wäre auch im tiefsten Punkt der Zitrone der Fall, also ist die Bedingung nicht hinreichend, sondern nur notwendig, denn sie gilt ja auch im Minimum). In beiden Fällen ist das totale Differential der Funktion (1) gleich Null.

In Punkt B erkennt man hingegen, dass eine Erhöhung des Wertes von $y$ den Funktionswert ansteigen lassen würde. Offensichtlich befindet man sich in B also noch nicht auf dem höchsten Punkt der Zitrone.

Infolge der Budgetrestriktion, die sich wie eine Gerade wie e in der Abbildung darstellt, sind nun aber keine unabhängigen Bewegungen ${\rm{d}}x$ und ${\rm{d}}y$ möglich. Eine Änderung von $x$ ist über das Verhältnis der Güterpreise (Steigung der Budegetgerade) mit einer entsprechenden Änderung von $y$ verbunden:

$$y = {E \over {{p_y}}} - {{{p_x}} \over {{p_y}}}x \tag{2}$$ $${{dy} \over {dx}} = - {{{p_x}} \over {{p_y}}} \tag{2a}$$

Graphisch gesehen ist das gleichbedeutend damit, dass man die Zitrone senkrecht über e durchschneidet. Gesucht wird nun der höchste Punkt der Schnittkante.

Gleichung (2a) in (1) eingesetzt liefert

$$\cfrac{\cfrac{\partial U}{\partial x}}{\cfrac{\partial U}{\partial y}} = \cfrac{{p_x}}{{p_y}}\tag{3}$$

oder in Worten(s.a. Lagrange-Methode für eine elegantere Methode):

Eine alternative Interpretation ist möglich anhand der grafischen Darstellung von Indifferenzkurve und Budgetgerade ( Punkt P in Abb. 4): Auf der Indifferenzkurve ist die Änderung des Nutzens ${\rm{d}}U$ ex definitione null. Ihre Steigung kann somit nach (1) angegeben werden als

$$\left| {{{{\rm{d}}y} \over {{\rm{d}}x}}} \right| = \left| {{{{{\partial U} \over {\partial x}}} \over {{{\partial U} \over {\partial y}}}}} \right| \tag{4}$$

Die höchste Indifferenzkurve wird dort erreicht, wo die Budgetgerade eine Indifferenzkurve tangiert. Tangieren können sich Indifferenzkurve und Budgetgerade nur, wenn sie die gleiche Steigung ${{dy} \over {dx}}$ besitzen (denn sonst würden sie sich ja schneiden). Die Steigung der Budgetgerade aus (2a) muss also mit der Steigung der Indifferenzkurve aus (4) übereinstimmen:

$$\cfrac{\cfrac{\partial U}{\partial x}}{\cfrac{\partial U}{\partial y}} = \cfrac{{p_x}}{{p_y}}\tag{5}$$